Lemur Math
Mike Lee, of Delicious Monster fame, has a thrown up a tantalizing post concerning Core Animation and lemurs. Being a member of the Founding Troop myself, and an avid lover of OpenGL and Core Animation, I just had to check it out.
You'll notice this value is very close (relatively speaking) to the magical 2500 number that Mr. Lee came up with. Upon close inspection it gives a pretty smooth curve, and is mathematically derivable. Disclaimer: I have no idea if this is right, but I suspect it works.
Mike offers up a fantastic way of leveraging Core Animation to almost perfectly capture the essence of the Dashboard-liquifying, delicious flips the iPhone pulls off. Now then, while I am totally not the biggest math buff, I do have some background in the mathematics behind computer graphics, so I thought I'd offer up a more in depth explanation of the "Newmanian Physics" at work here.
So, let's dive right in.
Mike begins the breakdown of the actual numbers process thusly:
Luckily I used to work with this insane genius named Lucas, who discovered that if you put a very small value into "m34" of Core Animation's CATransform3D struct, then scale the layer just right, you get a decent facsimile of the iPhone flip.
Since m34 doesn't sound very good in conversation, I think of this at the "Newman factor." The resulting distortion is, therefore, "Newman distortion," and the units in which it is adjusted are Newmans. One Newman is equal to the inverse of the distortion, which I'm pretty sure is math-speak for transform.m34 = 1/distortionInNewmans. In other words, the more Newmans you have, the less the distortion.
If we look at the documentation for the CATransform3D struct (hidden at the bottom of CALayer mind you), we notice that it is simply a struct representing a 4x4 matrix of CGFloats. These are logically numbered as most elements of matrices are - an 'm', followed by the row number, and then the column number. Thus, the Newman factor, as described by Mike corresponds to the third row and fourth column of our 4x4 matrix.
Now then, the more pedantic among you might notice that we are using a 4x4 matrix, and not a 3x3 matrix as would be logical given that we are in 3D space - that is, we are working with x, y, and z components, and that in Mike's example we are actually working with this seemingly useless fourth column vector to produce the desired effect. This fourth column vector (m14, m24, m34, and m44 for those keeping track) is where our adventure starts.
Homogenous Coordinates
So, in math, as in computer graphics, this additional vector constitutes what are called homogenous coordinates. Roughly speaking, this equates to representing an N-D matrix using an N+1-D matrix, in order to capture an affine transform into a matrix form. Since modern graphics APIs work with matrices, modern graphics hardware is designed to work with matrices at a blindingly fast rate. Thus, in order to optimize affine transformations, being able to express them as matrices is extremely important.
Now then, I know what you are saying to yourself. Elliott, what the hell is an affine transformation? Glad you asked! At it's most basic level, an affine transformation is a linear transformation, followed by a translation. Linear transformations in N space are represented by a single NxN matrix. The follow up translation is represented by a single column vector (in matrix form) which is where the additional column comes from. Now then, you are probably wondering about the additional row - this row represents a projection vector.
I'll explain if you are interested, if not, you can safely skip this part, just know that the projection vector is important for OpenGL/DirectX, and that it results in the additional row - and completion of our 4x4 matrix.
Perspective Projection
Now then, the addition of the fourth coordinate (for each column vector, representing a point in space), means that we are technically working as if we were in 4D. This is useful for projection of a 3D scene, as we can refer to any point by it's 4D coordinates (x, y, z, w). Now then, assume we have two planes. We can refer to these two planes by their value of w, as that is the only actual thing that varies between them. So, if we refer to the difference between these two planes in terms of w, let's say, w = 1 for one plane, and w = k for another plane. It doesn't really matter what k is, just that it isn't (or it could be) 1.
Now then, our point can be expressed on either plane using the same x, y, and z coordinates so long as they are expressed correctly in terms of w = 1, that is that w = 1 is the base for the projection. Thus to relate the two points, (x, y, z, 1) and (x, y, z, k) we can simply divide each coordinate by k.
So, we get - (x, y, z, 1) == (x/k, y/k, z/k, 1). Pretty simple right? Awesome. As I said before, for our purposes, this doesn't really matter, but if you are really curious, this is very important in perspective projection, i.e. the effect of an object that is "farther" from you being projected at a smaller ratio. This additional row allows you to model this perspective projection into the matrix model, which, as before, is very useful.
Does Your Head Hurt Yet?
Alright! So now that I've justified to you that 4x4 matrices are necessary, we can continue with this lemury math lesson. Looking back to what Mike talked about, we see that the component at the third row and fourth column is being modified to create this effect. As per above, this corresponds to the additional translation in our affine transformation to the z coordinate.
This actually turns out to be an exact equivalent of a common OpenGL command - glTranslate3f(x, y, z) on the current matrix, which is actually the identity, as per Mike's source code. In addition, this is applied as a sublayer transformation, which means that it affects all of the sublayers on the layer it is set on, but of course, not the actual layer. The layer that this is set on, is in the fact the content view's layer, which means that this transformation happens to -- tada, the images.
But the real question, is what does this actually do? Great question. This is the first part, of a [not-so] tricky two part matrix multiplication. You see, this translation does not in fact produce the actual flip. It is simply a perspective correction in the form of a translation after another component of this single affine transform. That's right, the power of Core Animation and math combine to let you do amazing things with a single transform. Your graphics card can do a freakin' bazillion million of these a second. The other part, coincidentally, is a rotation around the Y-axis, just as Mike discussed Dashboard widgets perform. This matrix is fairly common, and is useful to keep in mind when working with Y-axis rotations.
Where a is the angle of rotation, in our case, 180 degrees or π radians.. So, turning back to the example at hand. The other part of the affine transformation is handled in the form of flipAnimation from Mike's code. This code proceeds to rotate the front view and back view (in this case, two different images) in opposite directions so as to give the sensation of the one image flipping "over" to reveal the other image. As per Mike's post, in reality this would cause the object (an image) to actually move towards us. However, what we expect and what we get aren't quite in sync. Since a computer display is just a projection of these images, we get a rather dull and uninteresting simple y-axis rotation, where we can't actually notice that the image should be moving towards us. If you imagine several planes, each one representing a computer display, the image would have realistically moved between one plane and another plane in the Z-direction (in this case, positive Z, coming out of your computer display, and thus representing the expected forward movement).
@finally
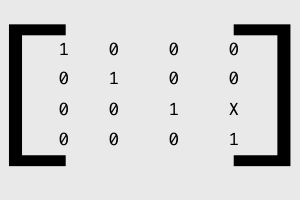
Alright, so now we have discovered the source of the majority of the flip, but remember, we still have that little Z translation floating around. So, if we combine the two to create our final affine transformation matrix, we get a matrix that looks like this. Let's define X as (1/DN).
Where DN is Distortion in Newmans. Now, you might notice that the inverse of distortion in Newmans is actually negative! This is pretty surprising, as Mike definitely set the distortion in Newmans to be the positive inverse of DN. How did this happen? Well, if we split this matrix back into the two matrices that formed them, we get:
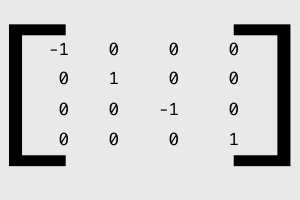
For the rotation. And
For the translation. Notice, still rocking the positive 1/DN. However, if you pull out that dusty old Linear Algebra textbook, and run matrix multiplication on these two matricies, you will notice that the negative values in the rotation matrix cause the 1/DN to become negative. In this case, this is interesting because we happen to have a positive Z increase from our Y-axis rotation that is being unrealistically removed from due to the projection onto our display. This, as Mike puts it, is fine when you are not rendering at full screen, but because you will clip over the edges on full screen, completely ruins the experience on a device like an iPhone.
So, what are we to do? Why, correcting for that inaccuracy seems like a good idea. That's exactly what Mike's code does. Since the final matrix actually creates that negative Z value that we are looking for, it will slowly move the image "away", creating a realistic perspective correction. This is noticed very easily by turning on Mike's debugging mode with a distortion value of ~2500, as in his example, and noticing the arc backwards created by the rotating origin. If you go back and comment out this code, you'll notice the origin follows a straight line across the X axis, resulting in the unrealistic transform we don't want.
So why does this work? Well, it's most easily demonstrated by looking at the application run in debug mode, however what we are really doing is defining a final value that we want Core Animation to have as the transformed Z value, and Core Animation smoothly animates to that value, which ends up rendering a curve as the component is "animated" over time.
If we look at the different values for distortion, we can see the differences in curves. as the ratio 1/DN gets lower and lower, we get a smoother and smoother Z-curve, obviously the point of being too smooth -- to where we don't get a realistic enough curve. To my knowledge, there is no magic ratio for this number. However, I've come up with an interesting little equation, which I think gives a decent recommended Newman Distortion value. I call it the Harris-Lee General Equation for Newman Distortion.
ND = 1 / ((Layer.Height / Layer.Width) / 1000)
This equation is a general equation, meaning it will work on all displays. However, rendering as an art is derived from the aspect ratio of the screen you are rendering on. In addition, we must have a consistent aspect ratio from the layer. With this in mind, we can actually derive a much more precise equation, which can be fine tuned for precise animations.
float layerRatio = 0.0;
if(Layer.Height > Layer.Width)
layerRatio = Layer.Width / Layer.Height;else if(Layer.Height <= Layer.Width)
layerRatio = Layer.Height / Layer.Width
float maxScreen = 0.0;
if(Screen.Height > Screen.Width)
maxScreen = Screen.Height;if(Screen.Width > Screen.Height)
maxScreen = Screen.Width;ND = 1 / (layerRatio / maxScreen);
Let's just plug in some values, based on my own display resolution (1440x900), and the size of the test image (300x400).
ND = 1 / (0.75 / 1440)
ND ~= 2000;
@conclusion
Hopefully, despite being long winded, I've shed some light on what exactly is going on. I'd like to thank Mike Lee, Lucas Newman, and Wil Shipley for pushing the envelope of what's possible with Core Animation. Apple for creating Core Animation. Jens Alfke, for inspiring me to become a Mac programmer, and finally my Computer Graphics professors for making me cram all this stuff into my head before they let me graduate in December.
Be back soon!
Edit: Updated with better matrices for posterity and non-embarrassment.
0 TrackBacks
Listed below are links to blogs that reference this entry: Lemur Math.
TrackBack URL for this entry: http://cocoadex.com/cgi-bin/mt/mt-tb.cgi/7


Awesome... Thanks so much for putting the time in to clear this up. Much appreciated!